作者：老喻
图文来源：微信公众号「孤独大脑」（ID：lonelybrain）

引子

关键不在于你游戏玩得多好，而在于你想玩什么游戏。——夸梅·阿皮亚

一、道理

「做难而正确的事情」，这个说法流行起来，也许是因为现在做事越来越难。

我欣赏这句话出处背后的故事和主角。但是，「做难而正确的事情」，会给正在做「难而错误的事情」的人们以错觉。

未必正确的事情，可能因为难而显得正确，这错觉和「丑男人很忠厚」一样不靠谱。

难而正确的事情，不是说做的时候难，而在于识别「正确的事情」很难，识别后做出选择更难。

本文将讲述一个「好运气的公式」：好运气 = 做对的事情 × 把事情做对

这个所谓公式，能解释很多「道理」，例如：选择比努力更重要。

• 「做对的事情」，是选择；

• 「把事情做对」，是努力。

创业者如元气森林的创始人，用贝叶斯定理的基础概率（或「基本比率」），来解释自己为什么要做饮料：

1. 饮料领域看起来很老土，但基数极大。中国饮料市场规模超过一万亿。

2. 对比而言，类似于 SaaS 市场，看起来很性感，可市场规模仅为百亿级别。

3. 所以，做饮料啃一小口也很大，做 SaaS 做到老大也很小。（这不代表创业公司不因为某个领域的增长空间而去做。）

投资人如芒格，他鼓励「去鱼多的地方捕鱼」：

1. 典型的例子如中国过去 20 年的地产大牛市，赢家们是因为正好撞进了鱼多的地方。

2. 而一旦鱼群退去，那些误以为自己是靠捕鱼能力赚钱的人就可能陷入困境。

聪明勤奋的雷军，悟到「顺势而为」，中年再出发去做智能手机，是一样的道理。 可是，智能手机市场虽然基数很大，为什么对绝大多数参与者并非意味着机会呢？如果是一个赢家通吃的市场，基数再大有什么用呢？

「时代是万位数、行业是千位数、个人专业是百位数」这类提法很生动，但确切地说：时代和个人之间，是一种乘积关系。

所以，我们应该再完整地看看「好运气的公式」： 好运气 = 做对的事情 × 把事情做对

• 做对的事情，是指基数大的市场，大趋势，大概率正确的事情；

• 把事情做对，是指鱼再多，也要和你有关系才有价值；

• 上面两项中间的「×」，是指你在鱼多的地方抓住鱼的匹配策略。

我喜欢用大白话将之总结为「运气三问」：

1. 天上为什么掉馅饼？

2. 馅饼凭什么掉在你的头上？

3. 你如何将这个馅饼吃进嘴巴里？

所以，智能手机对雷军来说也许是个馅饼，对罗永浩来说也许就是个陷阱了。（我很喜欢罗永浩，期待他早日回归科技界。）

我对这个话题感兴趣，是因为发现这个烂大街的道理，的确是许多高手们的「通用算法」。可是，这个道理并没有得到很好的解释和描述。

恰好这个道理背后，又有一些严密而有趣的计算。假如一个道理能够构建出一个模型，假如这个模型能够相对精确地被数学描述，没准儿真能成为「高手的公式」。

所以，本文是尝试做一件「将陈词滥调讲出新意」的事情，恰恰这类事情也是符合该公式的。

二、计算

人们对基础概率的忽视，经常带来现实中决策上的误判。

例如，你在街头看见一个美女貌若天仙，于是你猜：

a. 她是一位演员或者模特；
b. 她是一位普通的公司职员。

不少人会猜是 a，但，该美女是后者的可能性更大，因为公司职员的基数远大于演员。

为什么会出现误判？

一个是因为「鲜活效应」，二是因为忽视基础概率，三是颠倒了因果。

综合以上三点，人类喜欢根据鲜明的特征去套「规律」： 演员通常很美，所以，这位如此美的美女大概率是位演员。

再比如，你看到一项研究结果表明：3/4 的车祸发生在离家 25 英里以内的地方。于是，有人开始分析，离家近开车更不安全，是不是因为快到家了着急或者放松警惕？

这也是一个基础概率谬误。真相是 90% 的时间你都在家附近开车，发生车祸的概率当然更大。相比 3/4 的比例，实际上离家近开车可能更安全。

我还是用那个老掉牙的例子，来描述一下基础概率和相乘关系。

塔勒布在投资研讨会说：「我相信下个星期市场略微上涨的概率很高，上涨概率大概 70%。」但他却大量卖空标准普尔500指数期货，赌市场会下跌。他的意见是：市场上涨的可能性比较高（我看好后市），但最好是卖空（我看坏结果），因为万一市场下跌，它可能跌幅很大。

分析如下：

• 假使下个星期市场有 70% 的概率上涨，30% 的概率下跌。

• 但是，如果上涨只会涨 1%，下跌则可能跌 10%。

• 未来预期结果是：70% × 1% + 30% ×（-10%）= -2.3%。

• 因此应该赌跌，卖空股票盈利的机会更大。

好几个聪明的朋友对我说，这类计算太简单了，初中就学过。但其实并没有。

而且，之所以我老拿这个例子说事，是因为塔勒布的故事发生在华尔街，那帮顶尖聪明人也会在这个简单计算上犯糊涂。

姑且用上面这个计算套一下「好运气的公式」——

先看一下天上掉下来的是什么馅饼：

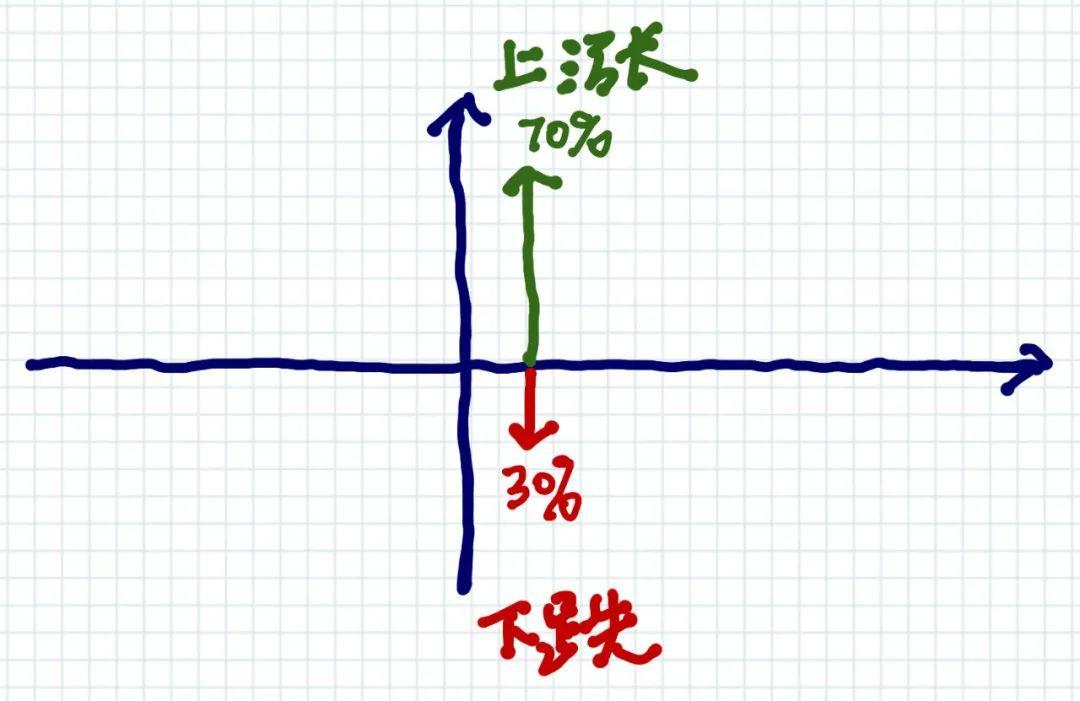
看起来是一个「上涨」馅饼。但是，根据公式我们知道，要计算的是乘积，所以，对好运气的计算应该是：

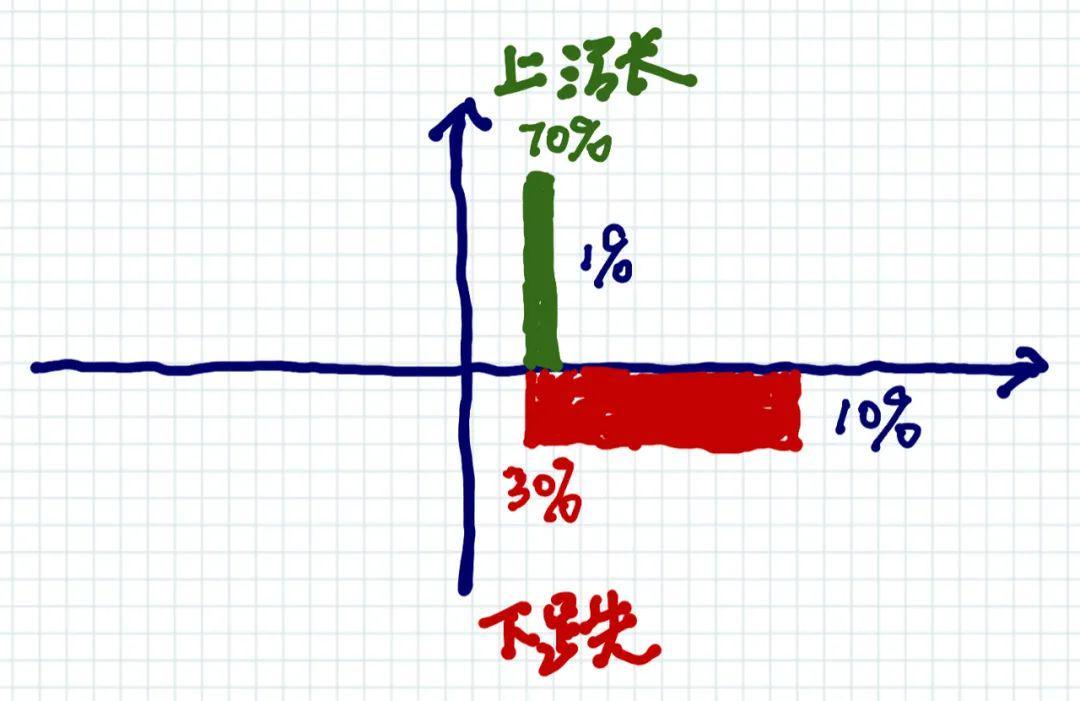
乘积的结果就是求面积。下跌的概率更低，但是可能下跌的幅度更大，所以下跌的期望值（红色面积），大于上涨的期望值（绿色面积）。

因为是乘积关系，所以长和宽是可以颠倒的。其隐喻是，哪怕是基础概率小的事情，也可以靠把事情做得更好而扳回来。一些专业领域的小而美的公司的确也是这样做的。

但是，假如二者的基础概率差 100 倍，要扳回来的代价就高很多。

为什么如此简单的计算，华尔街最聪明的人都会搞错呢？因为这里面的计算拐了两道弯，而我们的直觉更加适合解决拐一道弯的问题。

上面说了人类容易因为鲜活效应而忽视基础概率，那么，请允许我再拐一道弯：假如你在街头看见三位貌若天仙的美女在一起走，你认为她们是演员还是普通公司职员呢？ 我们的直觉，对于概率问题，通常是两头摇摆的。

再看一道让很多绝顶聪明的人也为难的题目：

某市八年级学生的平均智商是 100。为检验当地的教育水平，你随机选择了 50 名学生接受测试。第一个学生的智商测试得分为 150，请判断这 50 名学生的平均智商。 （摘自《思维的发现》 ）

答案难道不应该是平均数 100 吗？毕竟，那个智商 150 的孩子只是特例，也许会被得分较低的拉平。

正确答案应该是 101。

假如你错了，不必在意。当年这道题曾经考倒了一群精通概率的专家。

看似只是多了个「1」，差别其实很大。背后的有趣逻辑，提醒了我们基础概率与新证据之间的互动关系。

三、应用

我用公式来讲述一个世俗的道理，绝非是用所谓自然科学来套用社会科学。

理解基础概率，有助于我们摆脱人类典型性的依赖，避免由此产生的误判。

作为基于比较的直观动物，人类在某种意义上缺乏全局性。

所以，计算中的乘法，用面积来代表期望值，能帮助我们做出全面而理性的决策。

这也是一种基于「第一性原理」的思考。 这么做，并非完全基于基础概率来做判断。多个新证据的出现，会大幅修正基础概率，这正是贝叶斯定理的杠杆效应。

回到我们的「好运气的公式」：好运气 = 做对的事情 × 把事情做对

来看一下这个公式无处不在的应用。

1. 马斯克如何招聘？

马斯克招聘时，会问两个问题：

a. 你处理过哪些棘手问题。处理得怎么样？
b. 你在关键节点时如何做决策？

「解决难题」，在围棋里，相当于做死活题，很有挑战，但有最优解，或者说在具体情境、资源约束、时间限制下，有最优解；

「决策」则是指选点能力，例如左上角有个对杀，右下角有个大场，选哪个战场？然后才是具体解决问题。

二者也是乘积关系，最终价值取决于二者相乘的面积。

决策之难，不止是价值评估之难，你需要构建一个价值函数，还要代入数据估算；

决策更难之处是：要超越可以计算（例如有解的死活题）、能够看见的事物，去预见未来的结果，进而作出跨期决策。

以上这两种能力，是二位一体的。只会做局部死活题，容易「赢了每一场局部战役却输掉整个战争」；只会「选点」而不会做死活题……如果不会做死活题，根本谈不上「选点」这件事。

2. 大局观和资源分配

选点能力，就是找寻「什么是正确的事情」。

不管企业，还是个人，资源都是有限的。所谓选点，就是以全局视野，来找寻能够形成竞争优势的主战场，并分配资源。

做到这一点，需要非常艰难的思考。所谓「做艰难而正确的事情」，难在选择。大部分人会为了逃避这种艰难，而假装很辛苦地埋头去做事情。

难在哪里？难在大局观。

我将其概括为三种大局观：空间的大局观、时间的大局观、资源的大局观。

1）空间的大局观

就像下围棋，哪里重要下在哪里。

我从 AI 那里学到的最重要的一点，就是脱先：AI 永远去下全局中最重要的那一点，哪怕战场再激烈，一旦不是主战场了，立即转移，绝不纠结。

围棋毕竟还是一个完美的二维游戏，现实世界要复杂得多。 现实世界不会像围棋那样在某个维度上有极深的计算，而是由很多个维度的不那么深的计算交织在一起。

所以，我们只有用概率去评估，去计算各种变量的可能性，并通过加权计算期望值。

事物的概率，是一大堆交织在一起的模糊因果。 所谓「正确的事情」，本质上是去找寻大概率正确的事情。

2）时间的大局观

这一点更容易在投资和创业那里找到案例。

例如「长期持股」。价值投资者的长期主义，建立在他们的计算深度、以及预留的足够的安全边际基础之上。时间的大局观消除了短期的不确定性，令长期的确定性价值显露出来。

价值投资者的时间大局观，代表了概率的频率派。创业者的时间大局观，则代表了概率的贝叶斯派。

1. 创业者大多从小概率事件入手，然后随着时间不断优化概率。

2. 价值投资者更相信基础概率中的大概率事件，他们对「力挽狂澜」并不感兴趣。

时间的大局观，还应该包括对时代和周期的理解。

3）资源的大局观

指的是如何根据空间的大局观和时间的大局观分配有限的资源。

所谓战略，就是对有限资源的权衡取舍，以确保在优势地带形成局部的差异化优势，以追求达到某个浓度之后的「炸裂」。

3. 选择之后的努力

假如「选择」有用，那么，每个选择理论上都对应着几种不同的可能性，就像几个不同结局的平行宇宙。然而，在现实中，为什么命运似乎只是单线程地滑落？似乎并没有多个可能性的并行，哪怕只是在一念之间。

原因之一是，在已知变量里，个体的变量太微不足道了，如同一滴水落入大海般带不来任何改变，所以「选择」所带来的别的可能性并非没有，只是概率极低，可以忽略不计。

由此，选择也与浓度有关，进而与边界有关。所以，选择不仅是一个过程，还是一个系统。

个体的努力，必须基于一个相对封闭、但又能够与外界发生关系的系统。

就像制冷的冰箱，行驶的汽车。系统实现了局部的熵减，从而可以对外做功。

很多人去追逐时代的大机会，去学习，去混圈子，但是，假如没有自己的系统，没有手中的筹码，乘积仍然是零。

当我们的选择过于聚焦时，可能迷失在过于狭窄的空间里；
当我们的视野足够宏大时，选择的浓度不足以产生改变。

前者的浓度，需要靠空间来实现；
后者的浓度，则有赖于前者通过时间的叠加来实现。

关于选择和努力，聪明人最容易犯的错误是，试图将不正确的事情做成正确的事情。这并非不可能，但概率较低，费力很大。

例如，马斯克选择自己的路线，也是先自上而下思考，去找寻那些人类非做不可的事情。那些事当下也许是小概率的，但未来则可能是大概率的。

4. 乘号和匹配质量

陈春花教授大约讲过一段类似的话：

解决问题的价值，也取决于该问题的需求的强度。

如果用公式来表达，就是：价值 = 需求 × 解决。

这个公式和好运气的公式大致是一样的。

这就会引发出一个概念：匹配质量。

我在朋友发来的一段文字里看到这个概念，它尤其适用于个人成就，对于孩子的教育格外有启发。

个人成就 = 领域 × 个人努力。

一个人只有热爱自己的工作，才能够有持续的激情，长久的专注力。所以，长期主义从来都不是靠坚持的，而是靠高匹配质量下的兴趣和天性驱动。

围棋的关键是选点，企业的关键是选人。例如海底捞，服务员的热情不是靠培训出来的，而是靠选出来的。这是关于一个人的基础概率的命题。

有一项研究表明，那些职业生涯的早期，花了较多时间在「匹配质量」上的人，貌似起跑的时候有点儿游手好闲，兴趣太多，其实是在寻求对个人而言的全局最优点，一旦找到就会后来居上，势不可挡。

对于孩子的教育更是如此，漫长童年期的发明，就是为了让孩子在适度混乱的安全环境里，通过探索和试错，快速而低成本地实现自我认识。

可惜我们的教育大多做反了：我们花了太多时间教会孩子去提前学那些早晚都会并且成年后基本用不上的应试知识，却让他们在成年之后才开始思考：我喜欢什么？我擅长什么？我该做什么？

总结

本杰明·富兰克林说：20 岁时起支配作用的是意志，30 岁时是机智，40 岁时是判断。

什么是正确的事情？ 这是个非常复杂的问题。你需要有自己的价值评判标准，有目标，进而构建一个用于评估的价值函数。而且，「正确」总是一个概率化的问题，并且是一个渐进的过程。

什么叫把事情做对？ 同样非常复杂。这背后还是关于决策的话题，大之又大。也许我会在另外的文章里讲述上面的话题。

关于「好运气的公式」： 好运气 = 做对的事情 × 把事情做对，请记住「运气三问」：

1. 天上为什么掉馅饼？

2. 馅饼凭什么掉在你的头上？

3. 你如何将这个馅饼吃进嘴巴里？

这背后看似简单的数学计算，有着许多好玩儿让又让聪明人犯晕的题目。

请允许我用下面这道题作为 2022 年的新年礼物送给你：

有一个净重 10 千克的西瓜，含水量非常丰富，达到了 99%，放在太阳底下晒了一段时间后，含水量变成 98% 了，那么，这个西瓜现在多重？

好好算一下，你也许有意料之外的思考乐趣。

祝你 2022 年走好运，全家健康平安！

延伸阅读

老喻：比较是万恶之源
老喻：长期主义——做你余生中最重要的事
孟岩：运气和能力，究竟是谁在主宰我们的命运
知行读书会·《随机漫步的傻瓜》：我们控制不了「运气」，但可以主宰自己的行为

图文来源：公众号「孤独大脑」（ID：lonelybrain）
作者：老喻

本文章所载内容仅供参考，不构成投资建议。市场有风险，投资需谨慎，投资者应保持独立思考。详见《文章免责声明》。如转载使用，请参考《文章转载规范》。